중앙종거법(1/4법) 완벽 정리

현을 나누면 곡선이 보인다! ‘중앙종거법(1/4법)’ 완벽 정리

중앙종거법

안녕하세요! 지난번 편각법 포스팅에 이어, 오늘은 곡선 설치의 또 다른 방법인 ‘중앙종거법’에 대해 알아보려고 합니다.

현장에서 기계가 없거나 간편하게 곡선을 확인해야 할 때 아주 유용하게 쓰이는 방법인데요. 왜 이 방법이 ‘1/4법’이라고 불리는지, 그 마법 같은 비례 관계를 파헤쳐 봅시다!

 

1. 중앙종거법(1/4법)이란?

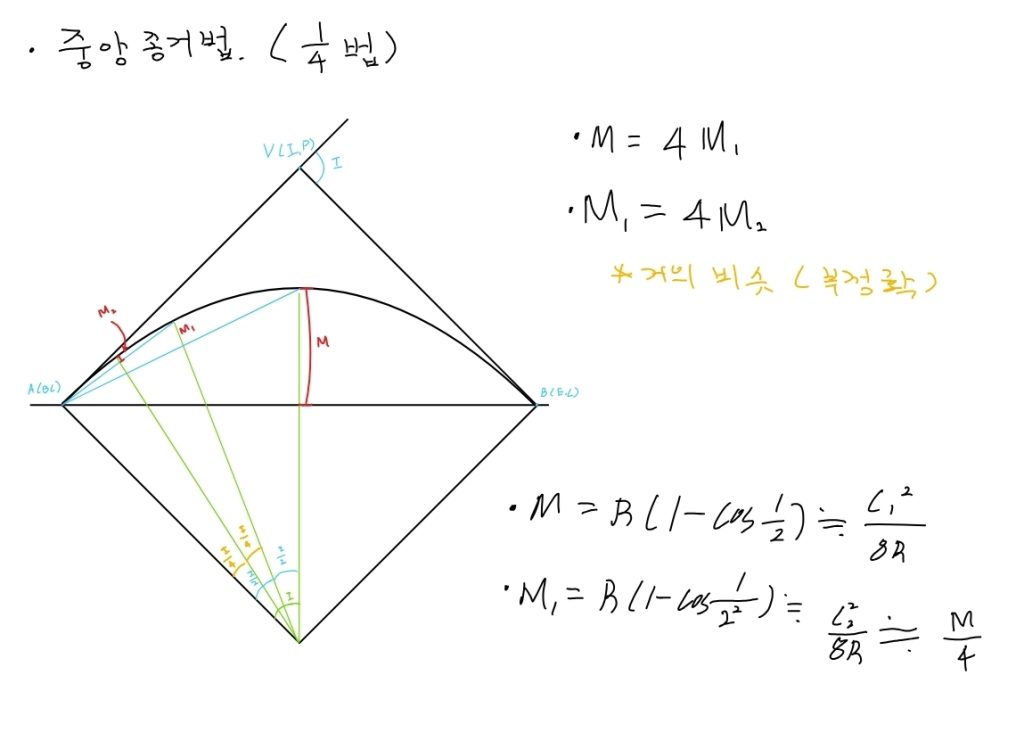
중앙종거법은 곡선의 현(Chord)을 계속해서 이등분하며, 그 중심에서 수직으로 뻗어 나가는 중앙종거(M)를 계산해 곡선상의 점들을 찾아가는 방법입니다.

* 특징: 계산이 직관적이고 방법이 간단합니다.

* 정밀도: 노트에 적힌 것처럼 “부정확(거의 비슷)”한 특성이 있어, 정밀한 도로 공사보다는 간이 설치나 검측용으로 주로 활용됩니다.

 

2. 핵심 공식: 1/4의 법칙

이 방법의 핵심은 단계가 넘어갈 때마다 중앙종거의 길이가 4분의 1로 줄어든다는 점에 있습니다.

* 비례 관계:

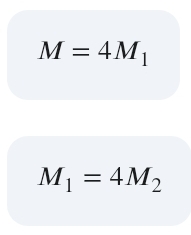
즉, 다음 단계의 중앙종거는 이전 단계의 1/4 크기가 됩니다.

* 수학적 계산:

 

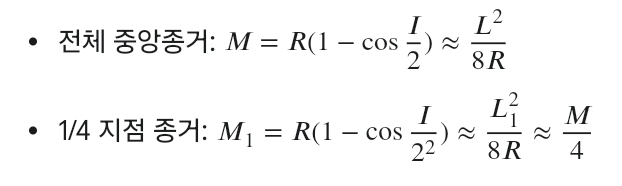
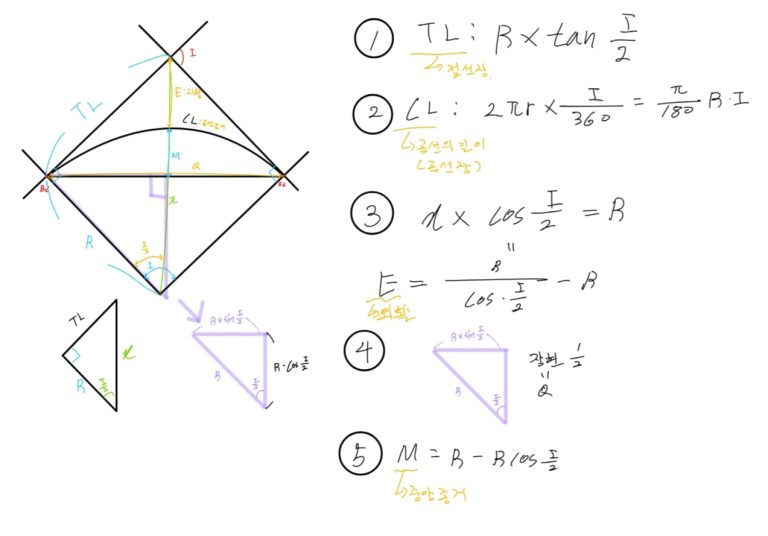
3. 그림으로 이해하는 설치 순서 🎨

노트의 그림을 순서대로 따라가 볼까요?

* 시점(BC)과 종점(EC)을 직선으로 연결해 커다란 현을 만듭니다.

* 현의 중심에서 수직 방향으로 계산된 M만큼 올라가 점을 찍습니다.

* 시점과 2번에서 찍은 점을 다시 직선으로 잇고, 그 중심에서 M1/4만큼 수직으로 올라갑니다.

* 이 과정을 반복(2등분)할수록 곡선은 점점 매끄러운 형태를 갖추게 됩니다.

4. 편각법 vs 중앙종거법, 언제 쓸까요?

* 편각법: “나는 오늘 완벽한 도로를 만들겠다!” 할 때 (높은 정밀도).

* 중앙종거법: “빠르게 곡선 구간을 확인하거나 대략적인 위치를 잡아야 한다!” 할 때 (간편함).

🌟 마치며

중앙종거법은 기하학적인 비례 원리를 이용한 아주 흥미로운 방법입니다. “길이가 1/4씩 줄어든다”는 포인트만 기억하면 실무나 시험에서도 절대 헷갈리지 않으실 거예요!

오늘 포스팅이 도움 되셨다면 공감과 댓글 부탁드려요! 다음에도 유익한 측량 지식으로 돌아오겠습니다. 😊

 

hnb

#측량학 #중앙종거법 #1/4법 #토목기사 #측량학정리 #곡선설치 #도로측량 #토목공학 #공부기록