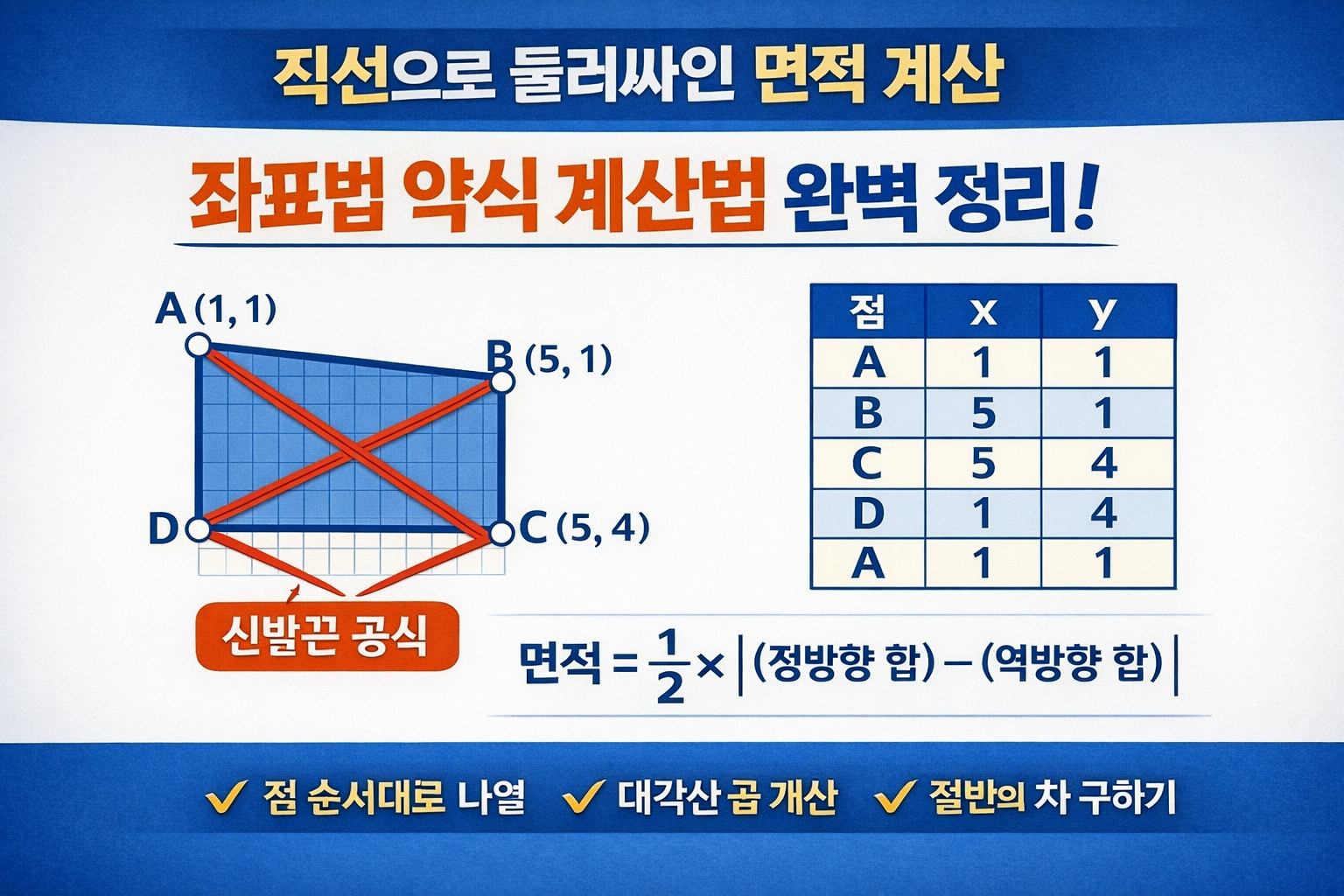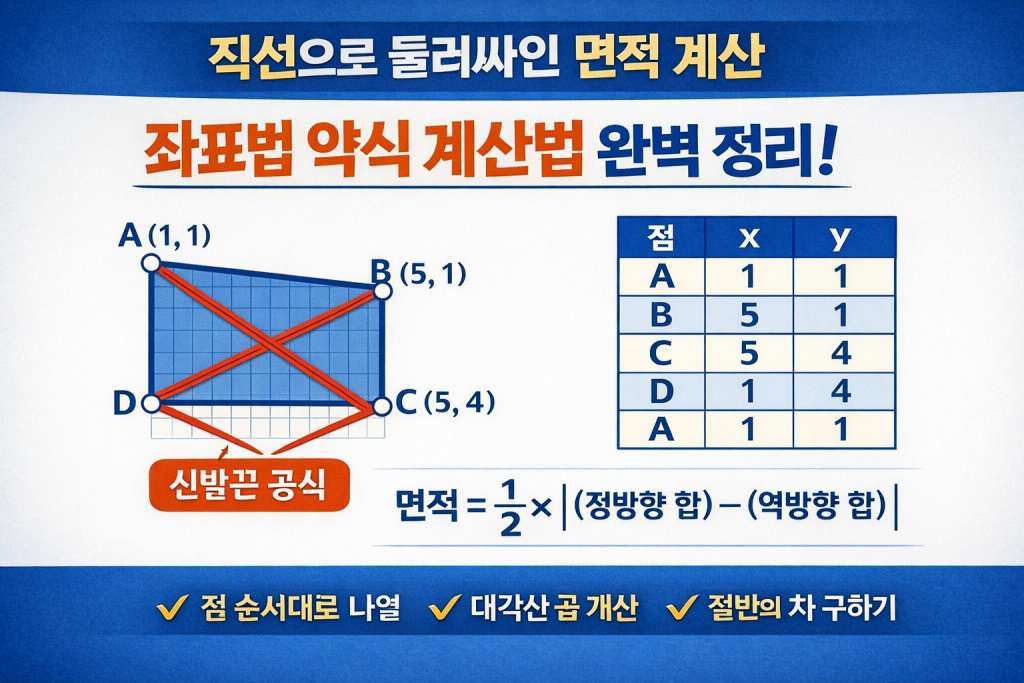
좌표법 약식 계산법은 직선으로 둘러싸인 폐합 다각형의 각 꼭짓점 좌표(x, y)를 이용해 면적을 계산하는 방법이다.
토지 경계, 대지 평면, 건축 도면처럼 경계선이 모두 직선으로 구성된 경우에 적용할 수 있으며, 삼각분할이나 각도 계산 없이 좌표의 곱과 합산만으로 면적을 산정할 수 있다는 점이 핵심이다.
이 방법은 측량 실무, 토지보상, 감정평가, 건설기술사·측량기사 시험 등에서 표준적으로 사용된다.
좌표법 약식 계산의 원리
다각형의 꼭짓점을 시계방향 또는 반시계방향으로 연속해서 배열한 뒤,
각 좌표를 교차 곱하여 생기는 값의 차이를 이용해 면적을 구한다.
구조적으로는
1 한쪽 대각선 방향의 곱을 모두 더하고
2 반대 방향 대각선의 곱을 모두 더한 뒤
3 두 값의 차에 1/2를 곱하는 방식이다.
이 계산 형태가 신발 끈을 교차해 묶는 모양과 유사해
‘신발끈 공식’이라고도 불린다.
좌표법 약식 계산 공식
꼭짓점이 (n)개인 다각형의 면적은 다음과 같이 계산한다.
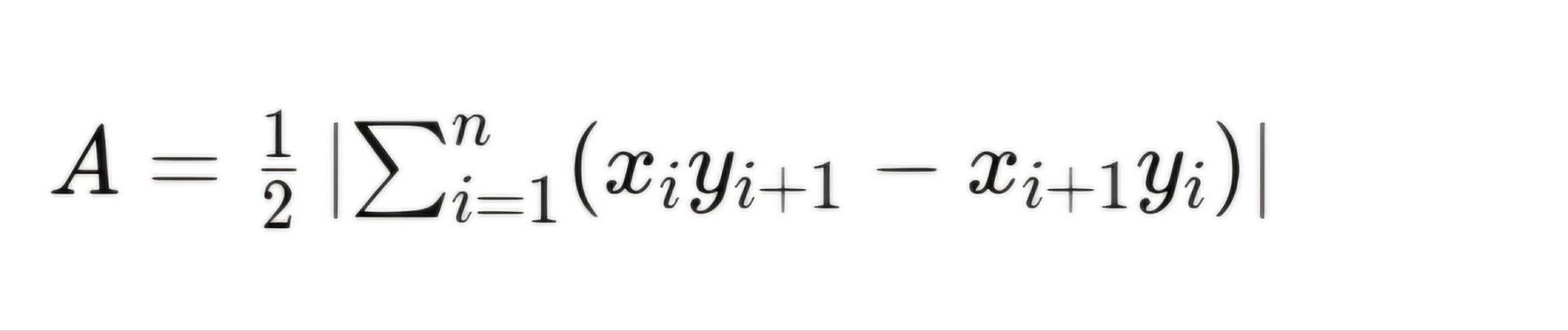
여기서 마지막 꼭짓점의 다음 좌표는 첫 번째 좌표로 연결한다.
계산 결과는 절댓값으로 처리해 방향에 따른 부호 문제를 제거한다.
표 계산 방식
현장과 시험에서는 공식보다 표 방식 계산이 훨씬 많이 사용된다.
1) 좌표 나열
꼭짓점을 경계 순서대로 나열하고, 마지막에 첫 점을 한 번 더 적는다.
| 점 | x | y |
| A | x₁ | y₁ |
| B | x₂ | y₂ |
| C | x₃ | y₃ |
| D | x₄ | y₄ |
| A | x₁ | y₁
2) 곱셈 계산
* 정방향 곱셈: (x_i × y_{i+1})
* 역방향 곱셈: (y_i × x_{i+1})
각 행마다 계산해 합산한다.
3) 면적 산출
![]()
계산 예제
다음과 같은 사각형이 있다고 가정한다.
| 점 | x | y |
| A | 1 | 1 |
| B | 5 | 1 |
| C | 5 | 4 |
| D | 1 | 4 |
| A | 1 | 1 |
정방향 곱의 합은
(1×1 + 5×4 + 5×4 + 1×1 = 42)
역방향 곱의 합은
(1×5 + 1×5 + 4×1 + 4×1 = 18)
따라서 면적은
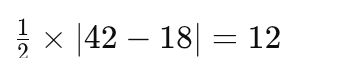
즉, 해당 도형의 면적은 12㎡이다.
약식 계산법이라 불리는 이유
좌표면적을 구하는 정식 방법은 삼각 분할이나 벡터 연산을 사용하지만,
좌표법 약식 계산법은 곱·합·차 계산만으로 면적을 구할 수 있어 계산 과정이 단순하다.
이 때문에 계산기, 엑셀, 수기 계산 모두에 적합하며
현장 실무와 시험에서 가장 많이 사용된다.
계산 시 주의사항
좌표 순서 오류
꼭짓점은 반드시 경계선을 따라 연속적으로 입력해야 한다.
방향 혼용 금지
시계방향과 반시계방향을 섞으면 계산이 틀어진다.
좌표계 확인
평면 직각좌표계에서만 정확하며, 위도·경도를 그대로 사용하면 안 된다.
Hhnbphnbpress.co