도로 위의 가이드라인 ‘편각법’ 정리 (공식/계산법)

도로 위의 가이드라인, ‘편각법’ 정리 (공식/계산법)

안녕하세요! 오늘은 토목/측량 분야에서 곡선 설치 시 가장 많이 활용되는 ‘편각법(Deflection Angle Method)’에 대해 핵심만 쏙쏙 뽑아 정리해 보려고 합니다.

공사가 진행될 때 곡선을 정확하게 설치하는 것은 안전과 직결되는 문제인데요. 그중에서도 정밀도가 가장 높다고 알려진 편각법, 왜 중요한지 그리고 어떻게 계산하는지 함께 알아볼까요?

1. 편각법이란? (Concept)

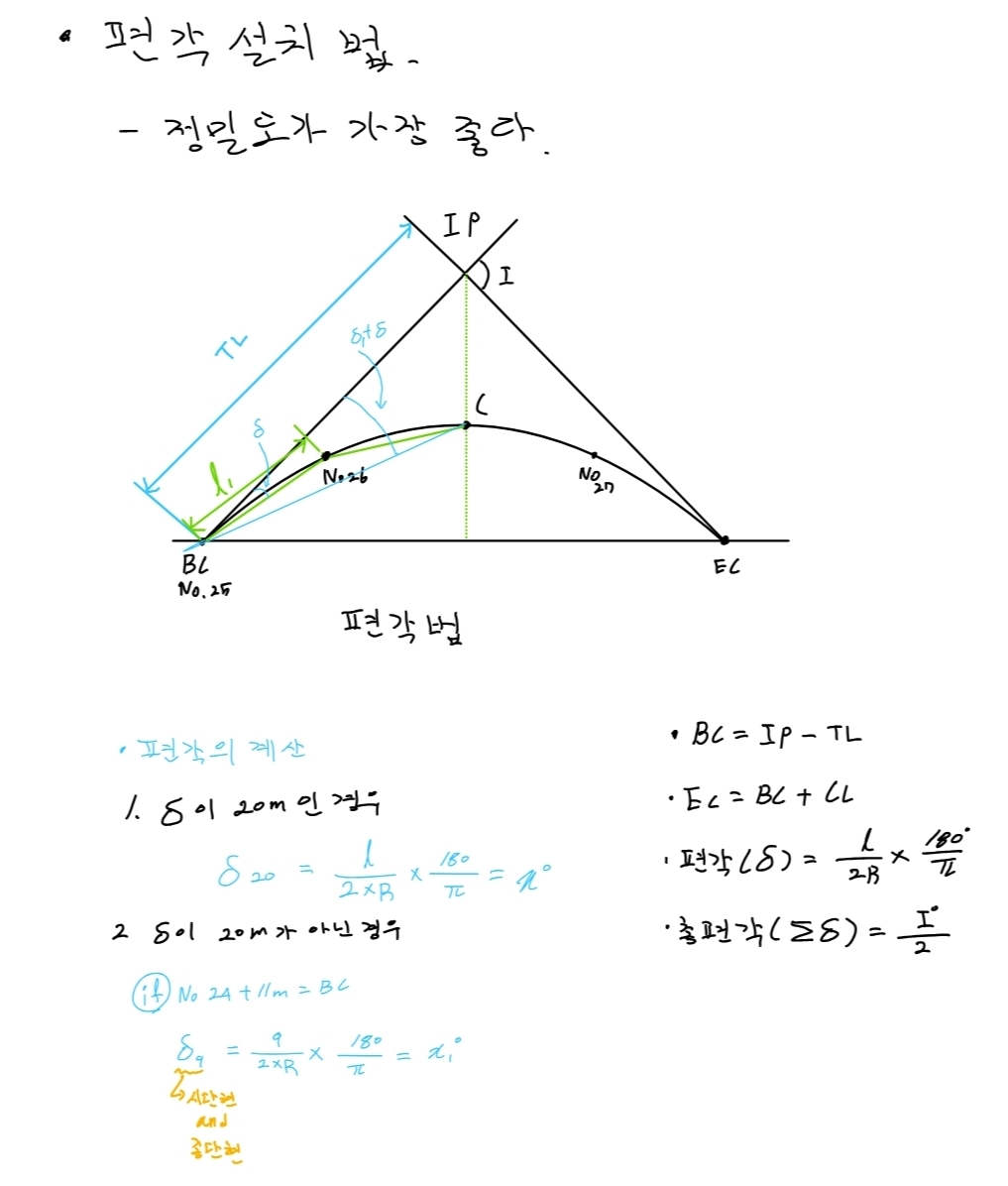
편각법은 곡선의 시작점인 BC(Beginning of Curve)에 토탈 스테이션이나 데오도라이트 같은 측량 기기를 세우고, 접선 방향을 기준으로 편각(\delta)을 계산해 곡선상의 점들을 하나씩 찾아가는 방법입니다.

* 특징: 다른 설치법에 비해 정밀도가 가장 좋습니다.

* 원리: 현의 길이(또는 호의 길이)와 편각 사이의 비례 관계를 이용합니다.

2. 곡선 설치를 위한 필수 공식

노트 속 핵심 공식들을 정리해 드릴게요. 시험 준비나 실무 하시는 분들은 필수 암기!

📍 위치 결정 공식

* BC (시점) = IP (교점) – TL (접선 길이)

* EC (종점) = BC (시점) + CL (곡선 길이)

> 주의: EC를 구할 때 IP에서 TL을 더하는 실수를 하지 않도록 조심하세요! 반드시 곡선 길이(CL)를 더해야 합니다.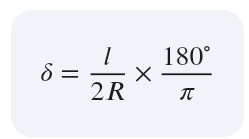

 

 

 

📍 편각 계산 공식

특정 구간의 길이(l)에 대한 편각은 다음과 같습니다.

 

* 총 편각 : 곡선 시점에서 종점까지의 전체 편각은 교각(I)의 절반인 I/2가 됩니다. (검산 시 필수 체크 포인트!)

3. 실전! 상황별 계산 노하우

실제 현장에서는 곡선이 딱 떨어지는 지점에서 시작되지 않는 경우가 많죠?

① 표준 간격(20m)인 경우

일반적인 구간은 l = 20m를 대입하여 계산된 20 값을 사용하여 일정하게 점을 찍어 나갑니다.

② 시단현/종단현이 발생하는 경우 (중요!)

노트의 예시처럼 BC 지점이 No.24 + 11m라면?

* 다음 정스테이션인 No.25까지의 거리인 9m(l값)에 대해서만 별도의 편각(9)을 먼저 계산해 줘야 합니다.

* 이것을 시단현이라 부르며, 곡선의 시작과 끝부분에서 발생하는 짧은 구간을 정확히 처리해야 전체 곡선이 완벽해집니다.

🌟 마치며

편각법은 공식만 보면 복잡해 보이지만, “호의 길이에 비례해 각도가 결정된다”는 원리만 이해하면 응용이 아주 쉽습니다. 특히 정밀한 도로 설계나 철도 측량에서는 빼놓을 수 없는 기술이죠!

오늘 정리해 드린 내용이 여러분의 학습과 실무에 큰 도움이 되길 바랍니다. 궁금한 점은 댓글로 남겨주세요!